propiedades de la esperanza matemática, de la varianza y desviación estándar

Esperanza matemática

                                                               

            La esperanza matemática (también llamada valor esperado)  de una variable aleatoria discreta, es el valor medio de infinitas observaciones, también puede interpretarse como un punto de equilibrio de la distribución de una probabilidad.

            La definición “esperanza matemática”  tiene su origen en los juegos de azar y hace  referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.

Constantes

La esperanza matemática de una constante es igual a esa misma constante, es decir, si c es una constante, entonces E[c] = c.

Linealidad

La esperanza es un, ya que:

                  

             (*)

            

por ende:

donde X e  Y son variables aleatorias  y a y b son dos constantes cualesquiera.

Nótese que (*) es válido incluso si X no es independiente de Y.

1. La esperanza matemática de una constante k es igual a la misma constante:

E (k) = k

Ejemplo : Aplicando la propiedad E (k) = k se tiene que

a) E (4)= 4

b) E (16) = 16

2. La esperanza matemática de la suma de varias variables aleatorias es igual a la suma de las esperanzas matemáticas de los sumandos:

E (X + Y) = E(X) + E (Y)

Ejemplo:

 Hallar la esperanza de las siguientes variables aleatorias:

X	1	2	3
P(X=x)	0,6	0,3	0,07

Aplicando la propiedad: E (X + Y) = E(X) + E (Y)

E(X) = [(1.0,6) + (2∙0,3) + (3∙0,07)]

              0,6+ 0,6  + 0,21 =

E(x) = 1,41

3. Un factor constante se puede sacar fuera del signo de esperanza matemática:

E (kX) = k ∙ E(X)

Ejemplo:

a)  E(X)= 1,5

E (4X) = 4 ∙ E (X)

4 ∙ E (X) = 4. 1,5= 6

4. E (aX + b) = aE(X) + b

Ejemplo: Sea X cualquier variable aleatoria discreta. Si la variable aleatoria 3X + 4 tiene esperanza 2 ¿Cuál es la esperanza de X?

Se tiene que E (3X + 4) = 1. Por consiguiente, aplicando la propiedad:

E (aX + b) = aE(X) + b

                     2 = E (3X+4)= 3E(X) + 4

                      3E(X) = 2 - 4= -2, es decir, E (X) = -2/3

Varianza

La varianza de una variable aleatoria es una característica numérica que proporciona una idea de la dispersión de la variable aleatoria respecto de su esperanza. Decimos que es un parámetro de dispersión.

La definición es la siguiente

:

Es, por tanto, el promedio teórico de las desviaciones cuadráticas de los diferentes valores que puede tomar la variable respecto de su valor medio teórico o esperanza.

En el caso de las variables discretas, la expresión se convierte en:

Mientras que para las variables continuas tenemos:

En ambos casos existe una expresión equivalente alternativa y generalmente de cálculo más fácil:

Una de las características de la varianza es que  viene expresada en unidades cuadráticas respecto de las unidades originales de la variable. Un parámetro de dispersión derivado de la varianza y que  tiene las mismas unidades de la variable aleatoria es la desviación típica, que se define como la raíz cuadrada de la varianza.

Propiedades de la varianza

1.    Var(X) ≥ 0

2.    Var(k · X) = k2 · Var (X)para todo numero real k.

3.    Var(k) = 0 para todo numero real k.

4.    Var(a · X + b) = a2 · Var(X) para todo par de números reales a i b.

5.    Var(X + Y) = Var(X) + Var(Y) únicamente en el caso que X y Y sean independientes.

Ejemplos

1)      Var (C) = 0.  Lo que indica la propiedad es que: La varianza de una constante es CERO.  La varianza mide la dispersión, claro está que una constante no puede tener dispersión,  por lo tanto la varianza es cero.

Ejemplo:

C=  4                    Siendo C una constante, entonces tenemos que:

Var (C) = 0

2)      Var(C.X) = C2 . Var(X)       Lo que indica la propiedad es que: La varianza del producto de una constante multiplicada por una variable, será igual a la constante elevada al cuadrado multiplicada por la varianza de la variable.

Ejemplo:

C= 6  ,  X=  4              Siendo C una constante y X una variable aleatoria, entonces tenemos que:

Var(C.X) = C2 . Var(X)

Var(6 . 4) = 62 . Var(4)

Var(24) = 36. 4

144=  144

3)      Sí  X y Z son variable aleatoria cualquiera:

Var ( X + Z ) = Var (X) + Var (Z) + 2 Cov ( X, Y )

Teniendo en cuenta que la covarianza (Cov) de dos variables independientes es igual a CERO. Sí  X y Z son dos variables independientes Cov ( X, Y ) = 0 por lo tanto:

Var ( X + Z ) = Var (X) + Var (Z)

La varianza de la suma  de dos variables independientes es igual a la suma de varianzas.

Ejemplo:

Var(X)= 3

Var(Z)= 9

Var ( X + Z ) = Var (X) + Var (Z)

Var ( X + Z ) = 3 + 9

Var ( X + Z ) = 12

Desviación estándar

            Se define como la raíz cuadrada de la varianza. 

Ósea se la varianza es= v(x)² la desviación estándar = √v(x)

La desviación estándar denotada con la variable SX, corresponde a la raíz cuadrada de la varianza tomada con signo positivo

            SX = + S2X

1.    La desviación estándar será siempre un valor positivo o cero Sx ≥ 0

2.    La deviación estándar es invariante ante cambios de origen SX + x = SX

3.    La deviación estándar se modifica ante cambios de escala: ScX = |c| SX

Ejemplo en general

Tú y tus amigos habéis medido las alturas de vuestros perros (en milímetros):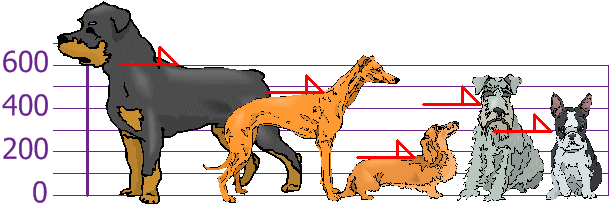

Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.

Calcula la media, la varianza y la desviación estándar.

Respuesta:

Media =	600 + 470 + 170 + 430 + 300	=	1970	= 394
	5		5

así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:

 

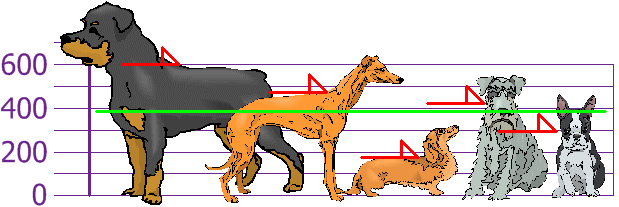
Ahora calculamos la diferencia de cada altura con la media:

 

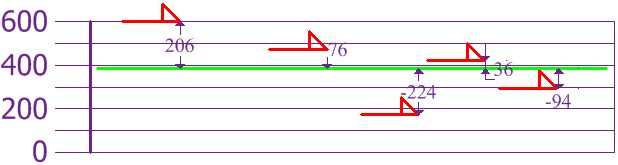
Para calcular la varianza, toma cada diferencia, elévala al cuadrado, y haz la media:

Varianza: σ2 =	2062 + 762 + (-224)2 + 362 + (-94)2	=	108,520	= 21,704
	5		5

Así que la varianza es 21,704.

Y la desviación estándar es la raíz de la varianza, así que:

Desviación estándar: σ = √21,704 = 147

y lo bueno de la desviación estándar es que es útil: ahora veremos qué alturas están a distancia menos de la desviación estándar (147mm) de la media:

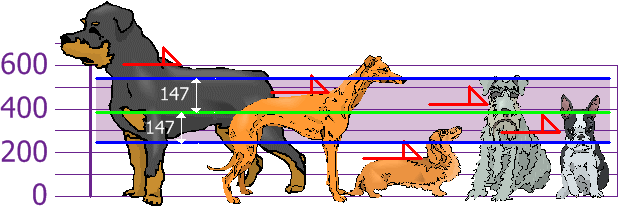
Así que usando la desviación estándar tenemos una manera "estándar" de saber qué es normal, o extra grande o extra pequeño.

Los Rottweilers son perros grandes. Y los Dachsunds son un poco menudos... ¡pero que no se enteren!

*Nota: ¿por qué al cuadrado?

Elevar cada diferencia al cuadrado hace que todos los números sean positivos (para evitar que los números negativos reduzcan la varianza)

Y también hacen que las diferencias grandes se destaquen. Por ejemplo 1002=10,000 es mucho más grande que 502=2,500.

Pero elevarlas al cuadrado hace que la respuesta sea muy grande, así que lo deshacemos (con la raíz cuadrada) y así la desviación estándar es mucho más útil.